¡Funciones!

Función exponencial

Paso 1

Inicia Microsoft Excel y abre un libro en blanco si no se abre automáticamente.

Paso 2

Haz clic en una celda para seleccionarla. Pulsa la tecla "=" para comenzar a crear una fórmula en la celda.

Paso 3

Escribe "Potencia (2,3)" y pulsa "Enter" o "Tab" para guardar el contenido de la celda y muévete a la siguiente celda hacia abajo o hacia la derecha, respectivamente. Observa que la celda muestra ahora la respuesta al primer número en el paréntesis elevado al segundo número en el paréntesis, o "dos elevado a la tercera potencia", que es igual a "8" en este caso.

Celdas de referencia

Paso 1

Inicia Microsoft Excel. Abre un libro de trabajo en blanco si no se abre uno automáticamente.

Paso 2

Haz clic en una celda en blanco y escribe el número "5" en la celda. Pulsa el botón "Enter" para guardar los contenidos de la celda y múevete a la siguiente celda.

Paso 3

Escribe el número "2" en la celda. Pulsa el botón "Enter" para guardar el contenido y muévete a la siguiente celda.

Paso 4

Pulsa la tecla "Igual" ("=") para comenzar a crear una fórmula para la celda.

Paso 5

Escribe la palabra "Potencia" seguido por el símbolo "Paréntesis abierto": mantén presionada la tecla "Shift" y pulsa el símbolo "(", ubicado en la misma tecla que el número 9 y, a continuación, haz clic una vez en la celda con el número "5" en ella. Presiona la tecla "," en el teclado y haz clic una vez en la celda con el número "2" en ella. Presiona la tecla de paréntesis de cierre: mantén presionada la tecla "Shift" y pulsa el símbolo ")", que se encuentra en la misma tecla que el número "0". Pulsa la tecla "Enter". Observa que el resultado es el número en la primera celda, un "5", elevado a la potencia en la segunda celda, un "2" o "25" en este caso. Ten en cuenta que si la primera celda es "A1" y la segunda celda es "A2", entonces la fórmula para la tercera celda debería verse como "=POTENCIA(A1, A2)" para que funcione correctamente.

Tomado de: https://techlandia.com/utilizar-funcion-exponencial-excel-como_182567/



--------------------------------------------------------------------------------------------------------------------------

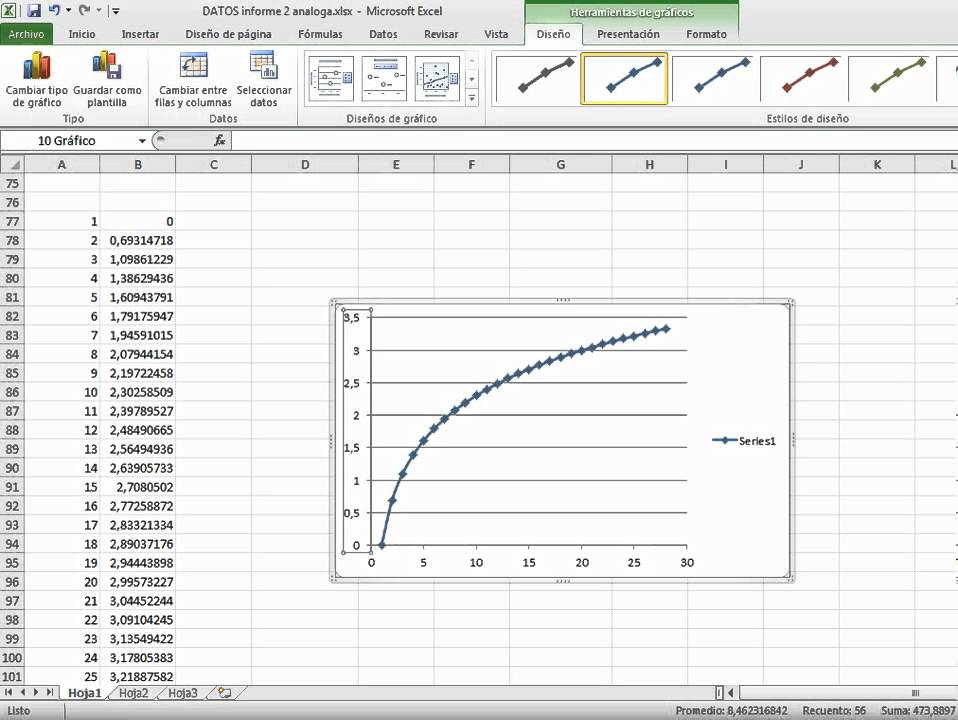
Funcion lineal

Primero escribimos en la celda A1(x) y en la celda B1(y).

Debajo de la variable x escribimos cualquier valor. Por ejemplo 98 y debajo 97 y debajo de la variable y se digita la formula  "=1,5*A2-1".

Oprimimos "ENTER" y se nos aparece el valor , ahora  nos ubicamos en el vertice inferior derecho y arrastramos hasta que lleguemos a -98.

Lo mismo hacemos en la variable y hasta llegar a  -98 .



Ahora seleccionamos  todo los de las dos variables y nos vamos a MENU  , insertar seleccionamos graficos y seleccionamos  dispersion , y luego seleccionamos dispersion  con lineas suavizadas .



Hacemos click ahi y nos aparece esto :



Como queda..

--------------------------------------------------------------------------------------------------------------------------

Función cuadrática

La forma general de una función cuadrática es f ( x ) = ax 2 + bx + c . La gráfica de una función cuadrática es una parábola , un tipo de curva de 2 dimensiones.

La parábola "básica", y = x 2 , se ve así:

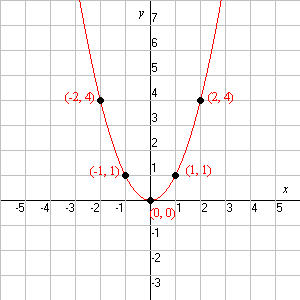
La función del coeficiente a en la ecuación general es de hacer la parábola "más amplia" o "más delgada", o de darle la vuelta (si es negativa):

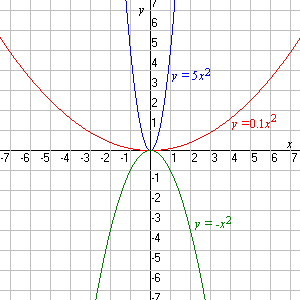
Si el coeficiente de x 2 es positivo, la parábola abre hacia arriba; de otra forma abre hacia abajo.

El vértice

El vértice de una parábola es el punto en la parte baja de la forma "U" (o la superior, si la parábola abre hacia abajo).

La ecuación para una parábola también puede escribirse en la "forma vértice":

y = a ( x – h ) 2 + k

En esta ecuación, el vértice de la parábola es el punto ( h , k ).

Puede ver como esto se relaciona a la ecuación estándar al multiplicarla:

y = a ( x – h )( x – h ) + k

y = ax 2 – 2 ahx + ah 2 + k

El coeficiente de x aquí es – 2 ah . Esto significa que en la forma estándar, y = ax 2 + bx + c , la expresión

nos da la coordenada en x del vértice .

Ejemplo:

Encuentre el vértice de la parábola.

y = 3 x 2 + 12 x – 12

Aquí, a = 3 y b = 12. Así, la coordenada en x del vértice es:

Sustituyendo en la ecuación original para obtener la coordenada en y , obtenemos:

y = 3(–2) 2 + 12(–2) – 12

= –24

Así, el vértice de la parábola esta en ( – 2, – 24).

El eje de simetría

El eje de simetría de una parábola es la recta vertical a través del vértice. Para una parábola en la forma estándar, y = ax 2 + bx + c , el eje de simetría tiene la ecuación

Dese cuenta que – b /2 a es también la coordenada en x del vértice de la parábola.

Ejemplo:

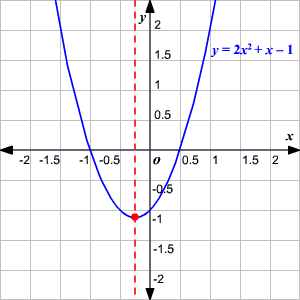
Encuentre el eje de simetría.

y = 2 x 2 + x – 1

Aquí, a = 2 y b = 1. Así, el el eje de simetría es la recta vertical

Intercepciones

Puede encontrar la intercepción en y de una parábola simplemente al introducir 0 para x . Si la ecuación esta en la forma estándar, entonces Usted solo toma a c como la intercepción en y . Por ejemplo, en el ejemplo anterior:

y = 2(0) 2 + (0) – 1 = –1

Así la intercepción en y es – 1.

Las intercepciones en x son un poco más complicadas. Puede usar la factorización , o completar el cuadrado , o la fórmula cuadráticapara encontrar estas (si es que existen!).

Dominio y rango

Como con cualquier función, el dominio de función cuadrática f ( x ) es el conjunto de los valores de x para los cuales la función esta definida, y el rango es el conjunto de todos los valores de salida (valores de f ).

Las funciones cuadráticas generalmente tienen la recta real de enteros como su dominio: cualquier x es una entrada legítima. El rango esta restringido a esos puntos mayores que o iguales a la coordenada en y del vértice (o menores que o iguales a, dependiendo si la parábola abre hacia arriba o hacia abajo).

Tomado de: https://www.varsitytutors.com/hotmath/hotmath_help/spanish/topics/quadratic-function